Cardiovascular Modeling
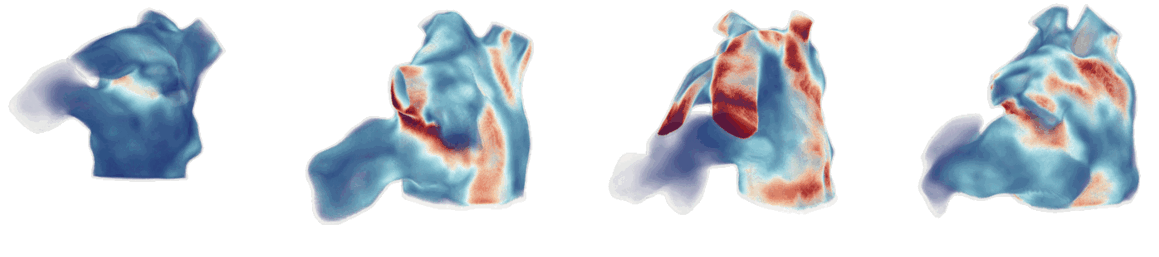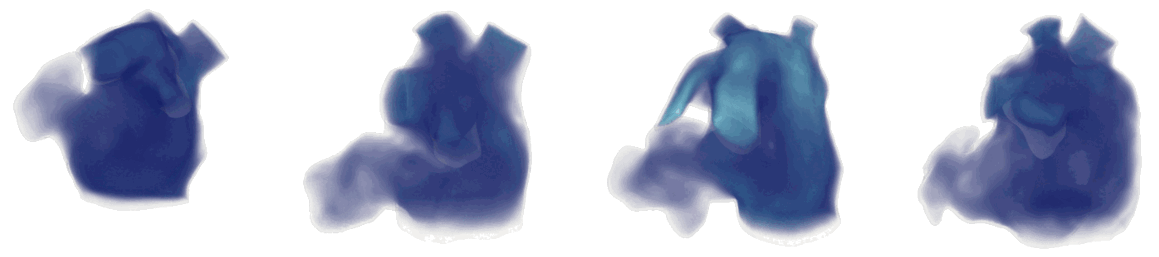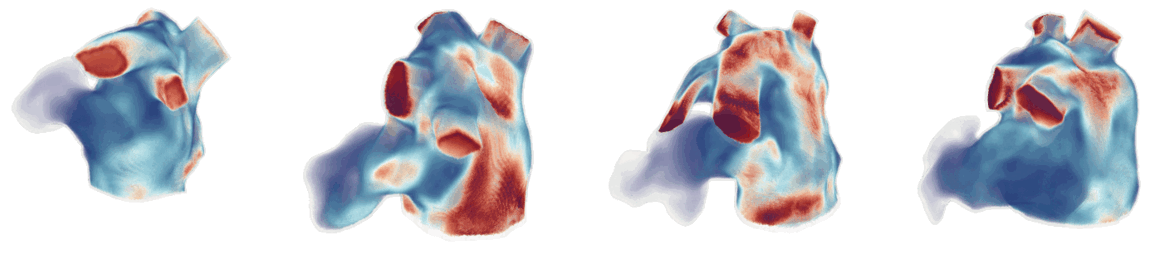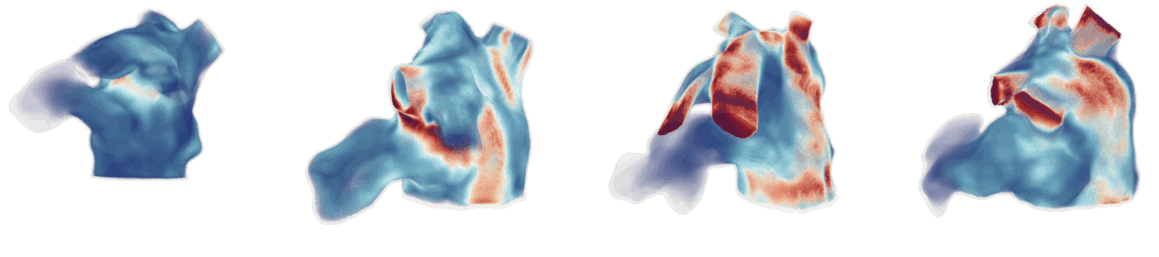
Figure 1: Cardiac fluid dynamics models of blood flow on patient-specific moving left atrial geometries.
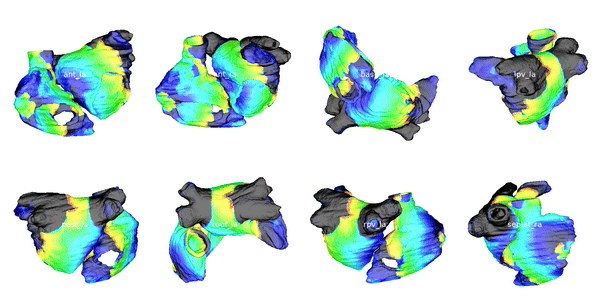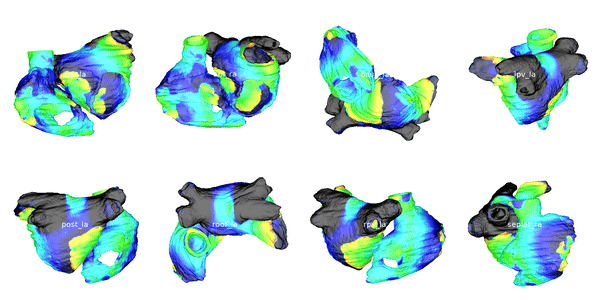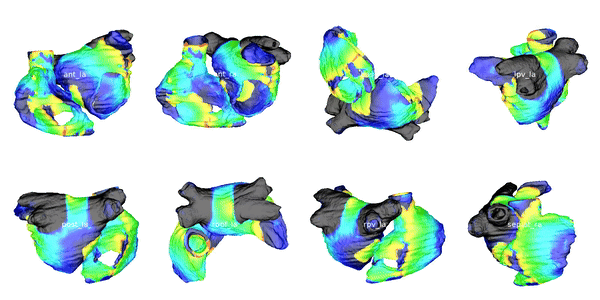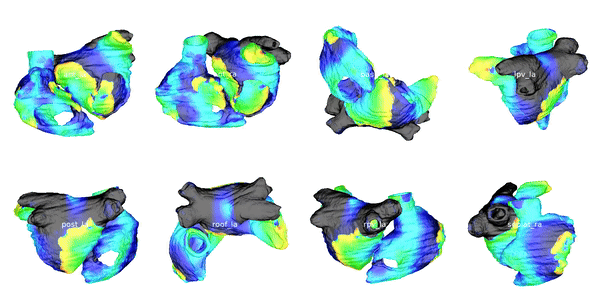
Figure 2: Cardiac electrophysiology (EP) simulations on patient specific biatrial geometries.
CFD simulations involve solving the Navier-Stokes equations using finite element methods, such as the Arbitrary Lagrangian-Eulerian (ALE) method to handle moving boundaries (Figure 1). The Navier-Stokes equations, governing the fluid dynamics, are given by:
$$\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} = -\nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{f}$$ $$\nabla \cdot \mathbf{u} = 0$$
where $\mathbf{u}$ is the velocity field, $p$ is the pressure, $\nu$ is the kinematic viscosity, and $\mathbf{f}$ represents body forces (e.g., gravity).
The ALE formulation introduces a mapping from a reference domain $\Omega_0$ to a time-dependent domain $\Omega(t)$. This mapping can be described by:
$$\mathbf{x} = \mathbf{x}(\boldsymbol{\xi}, t)$$
where $ \boldsymbol{\xi} $ are the coordinates in the reference domain $\Omega_0$ and $\mathbf{x}$ are the corresponding coordinates in the physical domain $\Omega(t)$. The mesh velocity
and the velocity field in the ALE formulation becomes:
This formulation ensures that the mesh deforms smoothly with the boundary motion, maintaining numerical stability in the simulation.
For cardiac electrophysiology (EP) simulations, the monodomain anisotropic reaction-diffusion equation is solved either using finite-element method (Figure 2) or the Lattice Boltzmann Method (LBM) (Figure 3). The monodomain equation is:
where
The LBM discretizes these equations by evolving particle distribution functions
where
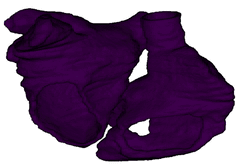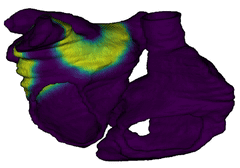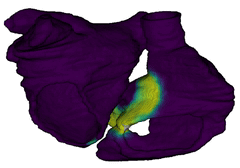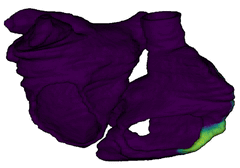
Figure 3: Cardiac electrophysiology (EP) simulations on patient-specific biatrial geometry using the Lattice Boltzmann method.