Riemannian Shape Analysis

Riemannian shape analysis studies the geometric properties of shapes by embedding them into Riemannian manifolds, where each shape corresponds to a point on a shape space manifold. A shape space manifold, $\mathcal{M}$, is equipped with a Riemannian metric $g$, which defines distances and enables geodesics—curves representing optimal shape transformations between shapes. Mathematically, given two shapes $S_1$ and $S_2$ on the manifold, their geodesic distance $d(S_1, S_2)$ reflects the minimal energy required for an optimal deformation to morph one shape into another:

$$d(S_1, S_2) = \inf_{\gamma \in \Gamma} \int_0^1 \sqrt{g(\dot{\gamma}(t), \dot{\gamma}(t))} , dt,$$

where $\Gamma$ is the set of all smooth paths connecting $S_1$ and $S_2$, and $\gamma(t)$ is a geodesic path parameterized by $t \in [0, 1]$.

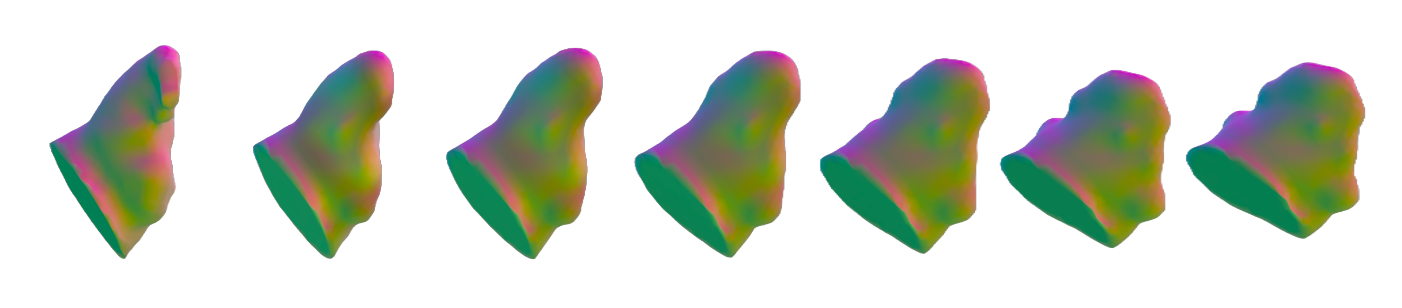
Figure 1: Geodesic between source shape and target shape of left atrial appendages (LAAs).

In medical image analysis, Riemannian shape spaces are used to study anatomical variability. For example, clustering left atrial appendages (LAAs) based on their geometric properties can aid in stratifying patients by anatomical risk factors for stroke. By representing LAAs as points on a shape manifold, one can use geodesic distances to cluster similar shapes and detect outliers:

$${ S_1, S_2, \ldots, S_n } \mapsto \mathcal{C}_1, \mathcal{C}_2, \ldots, \mathcal{C}_k,$$

where each $\mathcal{C}_i$ is a cluster of shapes. This approach enables automated classification, patient-specific risk assessment, and treatment planning, such as determining the optimal occlusion device for stroke prevention.