Mathematical Biology
Mathematical biology involves using first principles to simulate physiological systems and processes. My research has included work on:
Optimal Surgical Interventions for Fontan Patients
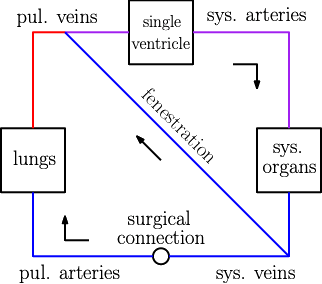
Reduced-order models of hemodynamics and oxygen transport in the Fontan circulation and the fenestrated Fontan circulation to optimize surgical parameters for maximized
Action Potential Propagation in Neuron Models
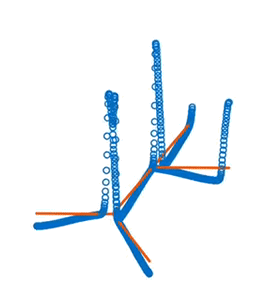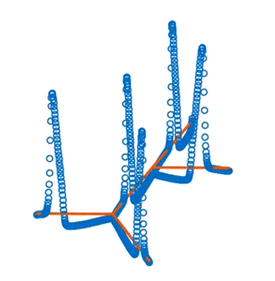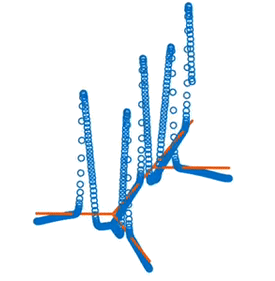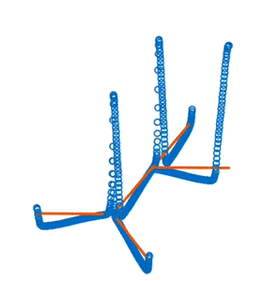
A generalizable framework for modeling short time scale dynamics in any given neuron geometry. Able to specify any tree structure and axonal and dendritic channel properties.
Modeling Circulation Hemodynamics under Hypergravity
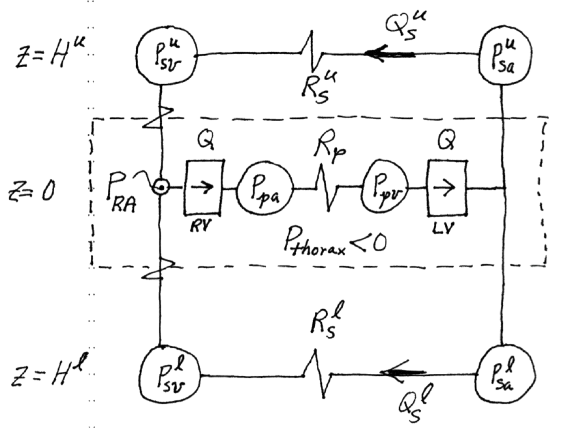
Constructing reduced-order models of the circulatory system with feedback control to incorporate the effects of hypergravity (e.g., during space flight acceleration or fighter jet acceleration) and calibrating/comparing with centrifuge experimental data to accurately predict G-tolerance. Presented at SIAM Life Sciences 2022 and SIAM Control Theory 2023.
Variable Heart Rate in a Pulsatile Circulation Model with Feedback Control
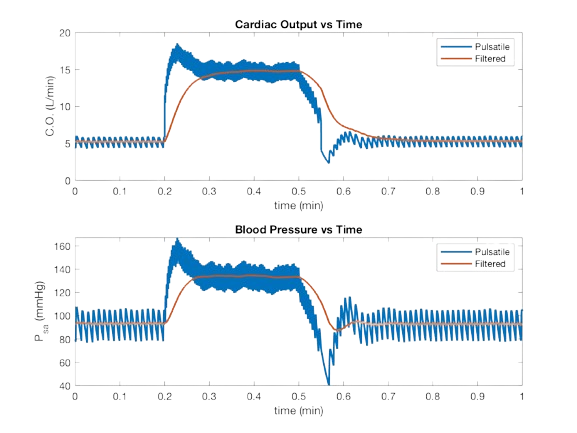
Incorporating feedback control elements (baroreceptor loop and SA node) into a pulsatile model with a time-varying heart rate function equipped with time-warping ODEs for compliance computations.
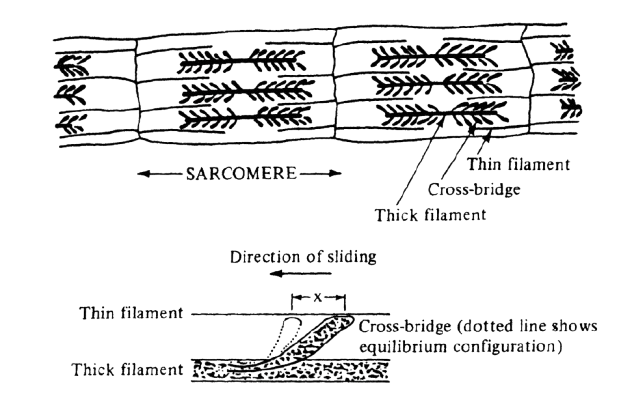
Mechanical Aspects of Crossbridge Dynamics during Muscle Contraction